問題5 ~ 落体の運動 (斜方投射)-04
落体の運動 (斜方投射)-04

問題
図に示すように、水平な地面すれすれに飛んできた質量 $m$ のボールがある。このボールを鉛直に立てられた薄い壁に向かって野球のバットで打ち返すものとする。但し、ボールは極めて小さいものとして、ボールの空気抵抗を無視し、ボールの回転はないものとする。
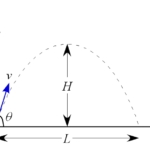
打ち返されたボールは、地面と $\theta$ の角度をなす方向へ速さ $v_0$ で飛び、その後、壁の先端すれすれの所を壁に垂直に飛び越えた。
重力の加速度を $g$ として、つぎの問いに答えよ。
(1) ボールが打ち返されたときから、壁の先端を通るまでに要した時間を求めよ。
(2) 壁の高さを求めよ。
(岩手大 改)

解答
運動方程式を立てる
まずは軸を設定し、

続いて作用する力を書く

運動方程式は
$x$ 方向: $ma_x=0$
$y$ 方向: $ma_y = -mg$
よって、加速度は
\begin{eqnarray*}
\begin{cases}
a_x=0 \\
a_y=-g
\end{cases}
\end{eqnarray*}
となる。
この2式から速度と変位を $x,y$ それぞれの軸に対して求めていく。
運動方程式を解く
ここで、初速度 $v_0$ を$x,y$ 成分に分解しておこう。

$x$ 軸について
\begin{eqnarray*}
a_x = \frac{dv_x}{dt} & = & 0 \\
v_x & = & C_1
\end{eqnarray*}
$t=0$ で $v_x=v_0 \cos \theta $ なので
\begin{eqnarray*}
v_x(0) = C_1 & = & v_0 \cos \theta\\
C_1 & = & v_0 \cos \theta
\end{eqnarray*}
よって
$$
v_x=v_0 \cos \theta= \mbox{一定} \quad \mbox{(等速度運動)}
$$
と表せる。
変位 $x$ は
\begin{eqnarray*}
v_x = \frac{dx}{dt} & = & v_0 \cos \theta\\
x & = & v_0 \cos \theta \cdot t +C_2
\end{eqnarray*}
$t=0$ で $x=0$ (原点)より
\begin{eqnarray*}
x(0) = v_0 \cos \theta \cdot 0 + C_2 & = &0 \\
C_2 & = &0
\end{eqnarray*}
よって
$$
x = v_0 \cos \theta \cdot t
$$
と表せる。
$y$ 軸について
\begin{eqnarray*}
a_y = \frac{dv_y}{dt} & = & -g \\
v_y & = & -gt + C_3
\end{eqnarray*}
$t=0$ で $v_y=v_0 \sin \theta$ より
\begin{eqnarray*}
v_y(0) = -g \cdot 0 + C_3 & = & v_0 \sin \theta \\
C_3 & = & v_0 \sin \theta
\end{eqnarray*}
よって
$$
v_y=-gt + v_0 \sin \theta
$$
と表せる。
変位 $y$ は
\begin{eqnarray*}
v_y = \frac{dy}{dt} & = & -gt + v_0 \sin \theta \\
y & = & -\frac{1}{2} gt^2 + v_0 \sin \theta \cdot t +C_4
\end{eqnarray*}
$t=0$ で $y=0$ より
\begin{eqnarray*}
y(0) = -\frac{1}{2} g \cdot 0^2 + v_0 \sin \theta \cdot 0 +C_4 & = &0 \\
C_4 & = &0
\end{eqnarray*}
よって
$$
y = -\frac{1}{2} gt^2 + v_0 \sin \theta \cdot t
$$
と表せる。
問に答える
問題文を見てみると、
(1) 壁の先端をすれすれに壁に垂直に飛び越えた。
物体の軌道を考えると、下図のように速度が変化する。

壁と速度が垂直になるのは最高点の時である。

従って、最高点になる時刻を求めればよい。
最高点では、$y$ 方向の速度が $0$ となる。その時刻を $t_1$ とすると
\begin{eqnarray*}
v_y (t_1) = -gt_1 + v_0 \sin \theta & = & 0 \\
t_1 & = & \frac{v_0 \sin \theta}{g}
\end{eqnarray*}
(2) 壁の高さ $=$ 最高点の高さであるから
\begin{eqnarray*}
y(t_1) & = & -\frac{1}{2}gt_1^2 + v_0 \sin \theta \cdot t_1 \\
& = & -\frac{1}{2} g \left( \frac{v_0 \sin \theta}{g} \right)^2 +v_0 \sin \theta \frac{v_0 \sin \theta}{g} \\
& = & -\frac{v_0 ^2 \sin ^2 \theta }{2g}+\frac{v_0 ^2 \sin ^2 \theta }{g} \\
& = & \frac{v_0 ^2 \sin ^2 \theta}{2g}
\end{eqnarray*}
コメント
・問題文の意味を理解することが重要。
・単に初速度 $v_0$、角度 $\theta$ の斜方投射運動。
・「壁に垂直に飛び越えた」の文で「最高点での速度は水平面と並行になる」ことが解るか
どうかがポイント。
・後は基本モデルの手順に従って必要な量を計算するだけの問題。




ディスカッション
コメント一覧
まだ、コメントがありません