問題4 ~ 落体の運動 (斜方投射)-03
落体の運動 (斜方投射)-03

問題
次の文中の空欄に当てはまる式を示せ。
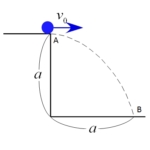
図のように、 $x=0, y=0$ の位置から角度 $\theta$、初速 $v [\mbox{m/s}]$ で、時刻 $t=0$ のとき打ち出された物体の運動を調べる。
重量加速度の大きさを $g [\mbox{m/s}^2]$ とすれば、時刻 $t [\mbox{s}]$ での物体の水平方向の位置は $x= \fbox{(1)} [\mbox{m}]$、鉛直方向の位置は $y= \fbox{(2)} [\mbox{m}]$ である。
さらに物体の最高点の高さ $H= \fbox{(3)} [\mbox{m}]$、水平到達距離 $L= \fbox{(4)} [\mbox{m}] $ である。
(中央大)

解答
運動方程式を立てる
まず軸については既に問題で設定されているので、そのまま利用する。
作用する力を書き込むと

運動方程式は
$x$ 方向: $ma_x=0$
$y$ 方向: $ma_y =- mg$
よって、加速度は
\begin{eqnarray*}
\begin{cases}
a_x=0 \\
a_y=-g
\end{cases}
\end{eqnarray*}
となる。
運動方程式を解く
この2式から速度 $v_x,v_y$ と変位を $x,y$ それぞれの軸に対して求めていくことになる。
事前準備として、初期条件である $v$ を$x$軸と$y$軸に分解しておくと

となる。
$x$ 軸について
\begin{eqnarray*}
a_x = \frac{dv_x}{dt} & = & 0 \\
v_x & = & C_1
\end{eqnarray*}
$t=0$ で $v_x=v \cos \theta$ なので
\begin{eqnarray*}
v_x(0) = C_1 & = & v \cos \theta \\
C_1 & = & v \cos \theta
\end{eqnarray*}
よって
$$
v_x=v \cos \theta = \mbox{一定} \quad \mbox{(等速度運動)}
$$
と表せる。
変位 $x$ は
\begin{eqnarray*}
v_x = \frac{dx}{dt} & = & v \cos \theta \\
x & = & v \cos \theta \cdot t +C_2
\end{eqnarray*}
$t=0$ で $x=0$ (原点)より
\begin{eqnarray*}
x(0) = v \cos \theta \cdot 0 + C_2 & = &0 \\
C_2 & = &0
\end{eqnarray*}
よって
$$
x = v \cos \theta \cdot t
$$
と表せる。
$y$ 軸について
\begin{eqnarray*}
a_y = \frac{dv_y}{dt} & = & -g \\
v_y & = & -gt + C_3
\end{eqnarray*}
$t=0$ で $v_y=v \sin \theta $ より
\begin{eqnarray*}
v_y(0) = -g \cdot 0 + C_3 & = &v \sin \theta \\
C_3 & = &v \sin \theta
\end{eqnarray*}
よって
$$
v_y=-gt+v \sin \theta \quad (-g\ \mbox{一定の等加速度運動)}
$$
と表せる。
変位 $y$ は
\begin{eqnarray*}
v_y = \frac{dy}{dt} & = & -gt+v \sin \theta \\
y & = & -\frac{1}{2} gt^2 +v \sin \theta \cdot t +C_4
\end{eqnarray*}
$t=0$ で $y=0$ (原点)より
\begin{eqnarray*}
y(0) = -\frac{1}{2} g \cdot 0^2 +v \sin \theta \cdot 0 + C_4 & = &0 \\
C_4 & = &0
\end{eqnarray*}
よって
$$
y = -\frac{1}{2} gt^2 +v \sin \theta \cdot t
$$
と表せる。
問に答える
さて、問題文を見てみると、
(1) 水平方向の位置、即ち、ある時刻 $t$ での変位 $x$ は
$$
x=v \cos \theta \cdot t
$$
(2)鉛直方向の位置、即ち、ある時刻 $t$ での変位 $y$ は
$$
y=-\frac{1}{2} gt^2 +v \sin \theta \cdot t
$$
(3) 最高点の高さ $H$ は
最高点では $y$ 方向の速度 $v_y$ がゼロになる。
その時刻を $t_1$ とすると、
\begin{eqnarray*}
v_y(t_1) = -gt_1+v \sin \theta &=& 0 \\
t_1 &=& \frac{v \sin \theta }{g}
\end{eqnarray*}
と表せる。
よって、最高点での高さ $H$ は
\begin{eqnarray*}
H= y(t_1) &=& -\frac{1}{2} g \cdot t_1^2 +v \sin \theta \cdot t_1 \\
&=& -\frac{1}{2} g \cdot \Bigl(\frac{v \sin \theta }{g}\Bigr)^2
+v \sin \theta \cdot \frac{v \sin \theta }{g}\\
&=& -\frac{1}{2} \frac{v^2 \sin^2 \theta}{g}+ \frac{v^2 \sin^2 \theta }{g} \\
&=& \frac{v^2 \sin^2 \theta }{2g}
\end{eqnarray*}
となる。
(4) 水平到達距離 $L$ について
$L$ は再び $y=0$ に戻った時の変位 $x$ である。
この時刻を $t_2$ とする。
変位 $y$ は
\begin{eqnarray*}
y &=& -\frac{1}{2} gt^2 +v \sin \theta t\\
&=& t \Bigl( – \frac{1}{2} gt + v \sin \theta \Bigr)
\end{eqnarray*}
と表すことができる。
$y=0$ となるのは、$t=0$ と $-\frac{1}{2} gt + v \sin \theta =0$ の時である。
$t=0$ はスタート時であるから、戻ってきたときは $-\frac{1}{2} gt + v \sin \theta =0$ となる。
よって、
\begin{eqnarray*}
-\frac{1}{2} gt_2 + v \sin \theta &=&0 \\
t_2 &=& \frac{2v \sin \theta}{g}
\end{eqnarray*}
となる。
従って、水平到達距離 $L$ は、
\begin{eqnarray*}
L=x(t_2) &=&v \cos \theta \cdot t_2 \\
&=& v \cos \theta \cdot \frac{2v \sin \theta}{g} \\
&=& \frac{2v^2 \sin \theta \cos \theta }{g}\\
&=& \frac{v^2 \sin 2\theta}{g}
\end{eqnarray*}
となる。
コメント
・斜方投射の基本的な問題である。手順を踏んで計算をしていけばよい。
・最後の(4)は、$\frac{2v^2 \sin \theta \cos \theta }{g}$と$\frac{v^2 \sin 2\theta}{g}$のどちらでもよいと思われる。
例えば、「さらに遠くに飛ばすための $\theta$ を求めよ」と言った設問があった場合に
三角関数は一つで表した方が考えやすいメリットがある。
・単位については問題の空欄の外に書いてあるので解答だけ記入すればよい。



ディスカッション
コメント一覧
まだ、コメントがありません